Understanding Qubits and Quantum Gates
Deriving Qubit and Quantum Gate using Schrödinger’s equation.
(If you don’t know what qubits and quantum gates are then I would recommend reading this article)
We have seen people talk about Qubits and Quantum gates in the field of Quantum Computing. But from where do we get these gates and quantum bits? Many say these qubits are electrons, and the quantum gates can be understood as analogous to the logic gates we use in normal computations. But this doesn’t help us to understand what they are and where they came from.
Interestingly, these Qubits and Quantum Gates can be derived from Schrödinger’s equation:
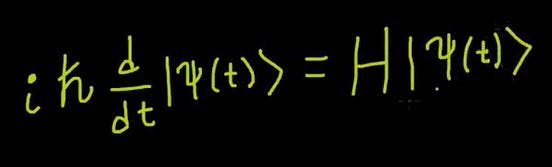( Even if you are not familiar with this equation it’s okay, it’s simple)
|Ψ(t)⟩ — Is a state of an electron at time t.
ℏ — Reduced Plank’s constant.
H — Hamiltonian operator (we will see this later).
i = Complex number.
| ⟩ is called a “ket”. It is just a way of representing any quantum state.
What is Hamiltonian Operator “H”
If you look at the left side of the Schrodinger equation, we have
Reduced Plank’s constant — Dimensions of Energy*time
i — Dimensionless quantity
\begin{equation}
\frac{d( |Ψ(t)⟩ )}{dt}\end{equation} — Dimensions of (1/time) (( |Ψ(t)⟩ is just a vector of two complex numbers).
Thus overall dimensions of the left side of the Schrödinger equation are dimensions of Energy!
To be a valid equation, the dimensions of both sides of an equation must be equal.
Now, if you look at the left side of the Schrödinger equation, we have
Hamiltonian Operator
|Ψ(t)⟩ — Dimensionless quantity
Thus our Hamiltonian operator must have dimensions of energy.
But what is H=?
For our ease consider the electron as a spherical charge.
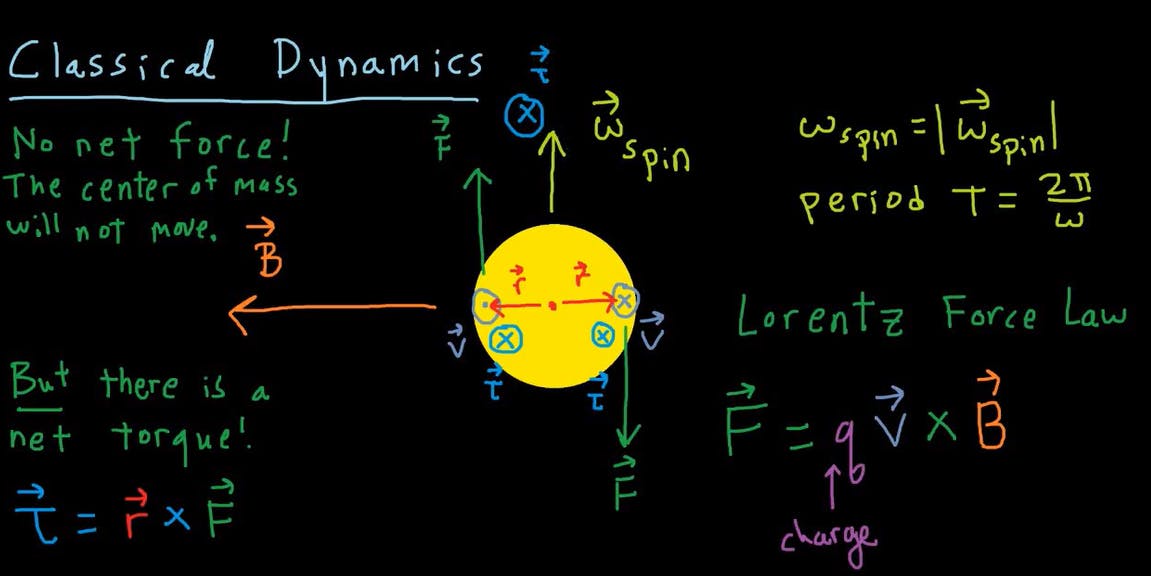When we keep this electron in magnetic field B, the total energy of that sphere is given as :
\begin{equation}U = (\frac{e}{2m})*(L.B) \end{equation}
where,
U = potential energy (here total energy)
e = charge of electron
m = mass of the electron
L = Angular Momentum
B = Magnetic Field
L.B is scalar multiplication of two vectors L and B.
Thus our “H” is some Quantum version of U
By putting this value of H in the Schrödinger equation and solving it by the matrix exponential method, we get the following equation:
(For those of you interested in the mathematics of solving the equation there is a link at the end of the blog !)
In the above equation, |Ψ(t)⟩ is the state vector of the electron at time t, and |Ψ(0)⟩ is the state vector of the electron at time 0sec and the exponential term is called matrix exponential. (If you don’t know what that is take a look at my notes given at the end or you can just think of it like a matrix )
Now, here’s the interesting part,
If you notice, the matrix exponential term is some kind of operation we are performing on state |Ψ(0)⟩ to get information about some state |Ψ(t)⟩ at time t secs. In the context of Quantum Computing, this matrix exponential term is called the Quantum gate (as you can see it performs some operation on state |Ψ(0)⟩, and the state |Ψ(0)⟩ is our Qubit on which the operation is performed!
If you liked this article I would be super excited if you hit the like button or share it with your curious friends. Anyway, thanks for reading have a great day.